Shape and Coordinates of the Universe

Let U be a 3-sphere centred on the origin (0, 0, 0, 0) with radius ρ_U.

Let ψ_U, θ_U, ϕ_U be spherical coordinates such that

w = ρ_U cos ψ_U
x = ρ_U sin ψ_U cos θ_U
y = ρ_U sin ψ_U sin θ_U  cos ϕ_U
z = ρ_U sin ψ_U sin θ_U sin ϕ_U

With a fixed value of ψ_U, θ_U and ϕ_U parametrize a 2-sphere with radius ρ_U sin ψ_U.  In two degenerate cases this is a point: 

Α (ψ_U = 0) = (ρ_U, 0, 0, 0)
Ω (ψ_U = π) = (-ρ_U, 0, 0, 0)

These points act as the centres of the non-degenerate 2-spheres (Α where 0 < ψ_U >= π/2, Ω where π/2 < ψ_U >= π). 

2-spheres centred on either Α or Ω can be defined entirely through a single value, ψ_h, corresponding to the fixed value of ψ_U.  The radius ρ_h of a 2-sphere h is ρ_U sin ψ_h.  θ values now act as the equivalent of latitude on this sphere, and ϕ values longitude. 

Visualising the 3-Sphere

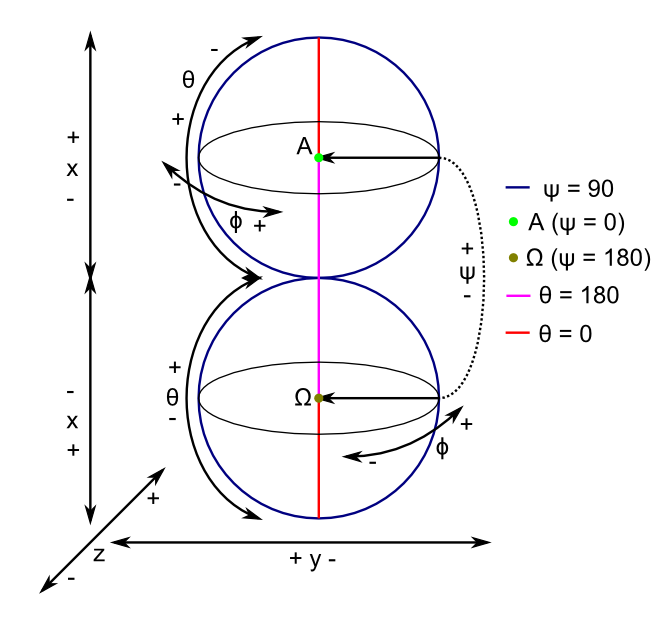
This diagram shows a visualisation of the 3-sphere based on "topological gluing" of two balls (referred to below as visualisation balls to more clearly distinguish them from 2-spheres within the 3-sphere).

Spherical Coordinates ψ θ ϕ

Consider a single 2-sphere centred on A or Ω.  θ is the "latitude" 0 to 180 degrees, ϕ the "longitude" 0-360 degrees.  Any point on the surface of the sphere can be defined with these coordinates. 

ψ represents the radius of the sphere.  ψ <= 90 places the sphere in the "top", centred on A, ψ >= 90 in the "bottom" centred on Ω.  ψ = 90 is where the largest 2-sphere lies, and equivalent to the surface where the two visualisation balls are glued.  This is the 3-sphere's "equator": just as at the equator of a 2-sphere there is the largest longitude circle, at the 3-sphere equator is the largest ϕ circle. 

Together these three coordinates can define any point within the 3-sphere.

Just as spherical coordinates produce degenerate cases on the 2-sphere (the points at the poles, where longitude is irrelevant) there are degenerate cases in the coordiantes of the 3-sphere.

ψ = 0 and ψ = 180 are degenerate, describing the two "poles" of the 3-sphere (points A and Ω).  At these points θ and ϕ are irrelevant.

θ = 0 and θ = 180 are also degenerate, describing two lines of varying ψ between A and Ω.  At these theta values ϕ is irrelevant.  θ = 0 or 180 is also a pole of any 2-sphere centred on A or Ω.

Cartesian Coordinates w x y z

ϕ θ ψ coordinates can be converted into 4 dimensional wxyz Cartesian coordinates (see above).

In the visualisation above the w coordinate is omitted.  It is indirectly represented by the change in visualisation ball and position within it.  A positive w is in the top ball, a negative one in the bottom ball.  Because w²  + x²  + y²  + z²  = ρ_U², w is also affected by xyz values and vice-versa.

Visually one of the balls is flipped upside down to demonstrate a touching point where the surfaces are glued.  In reality the same xyz values would be entirely equivalent and only the w value would separate them in the fourth dimension.  As an example A and O have the same xyz values, (0, 0, 0).  The only differ in w value: A is (r, 0 ,0 ,0) and  Ω is (-r, 0, 0, 0).

The unusual alignment of axes and positive/negative directions is mostly down to making this diagram the visual match to how I have the visualisation set up on the screen of the program I'm writing to sort all this out.

 

The Apex and Nadir

Vanans refer to A as the Apex.  It is the site of the Throne of God.  Ω is called the Nadir, the furthest possible point in the universe from the Apex, and is the site of the Vanan equivalent of Earth. 

The Heavenly Spheres

Between the Apex and Nadir are fourteen "heavenly spheres".  They are most easily visualised as spheres centred on A or Ω (or shells; they have thickness and an inner and outer radius).  From one of these points the nearest sphere is small.  More distant spheres start becoming larger, just as they would be in Euclidean 3D space.  However after a certain distance the spheres start to shrink again, contracting back until the opposite point is reached. 

The "spheres" are actually polyhedral in nature, formed from a set of vertices all lying on a sphere (the circumsphere).  They are constructed as follows:

First place a ring of N equally spaced vertices around the equator of the circumsphere.  Then place an additional two rings of N equally spaced vertices around the circles above and below the equator at latitude +/- 30.  The result is a polyhedron with 3N vertices arranged in 3 rings, in the form of a truncated bipyramid.

The insphere of such a polyhedra has the radius R cos 30, where R is the radius of the circumsphere, except when N < 6.  Where N < 6 the insphere is R cos (180/N).

Relative Distances

Assuming the distance between A and Ω is π (i.e. 3-sphere radius 1):

The distance of the circumsphere of the 15th “sphere” from the Apex is π.  The insphere of an N=47 polyhedron is r cos (π / 6).  Therefore the distance from A to the insphere is π cos (π / 6).

The circumsphere of the next closest sphere is equal to the insphere of the previous polyhedron.

ψ from distance is arcsine d  radians where d <= 1, or arcsine (d/π) + π/2 radians where d > 1.

n	N	Circumsphere (rn)	Insphere	Circumsphere Degree Distance
15	47	π	r15 cos (π / 6)	180
14	43	r15 cos (π / 6)	r14 cos (π / 6)	150.000
13	41	r14 cos (π / 6)	r13 cos (π / 6)	138.590
12	37	r13 cos (π / 6)	r12 cos (π / 6)	130.505
11	31	r12 cos (π / 6)	r11 cos (π / 6)	124.229
10	29	r11 cos (π / 6)	r10 cos (π / 6)	119.153
9	23	r10 cos (π / 6)	r9 cos (π / 6)	114.953
8	19	r9 cos (π / 6)	r8 cos (π / 6)	111.429
7	17	r8 cos (π / 6)	r7 cos (π / 6)	83.731
6	13	r7 cos (π / 6)	r6 cos (π / 6)	59.412
5	11	r6 cos (π / 6)	r5 cos (π / 6)	48.203
4	7	r5 cos (π / 6)	r4 cos (π / 6)	40.213
3	5	r4 cos (π / 6)	r3 cos (π / 5)	33.996
2	3	r3 cos (π / 5)	r2 cos (π / 3)	26.895
1	2	r2 cos (π / 3)		13.072

Sphere 15 has a circumsphere at Ω, and is as such a solid ball centred on Ω.  This is the sphere of Vana's "Earth" itself.

The N values of the spheres is the sequence of the first fifteen primes.  N = 2 does not actually produce a polyhedron, but a hexagonal series of six vertices on a plane.

Alignment

With yz as the reference plane, the spheres are aligned based on three factors: i (inclination), ω (angle of the ascending node) and σ (angle between the first vertex and the ascending node).

i rotates the equatorial plane of the sphere around the z axis.
ω rotates the equatorial plane of the sphere around the x axis.
σ places the first vertex relative to the intersection of the equatorial plane of the sphere and the yz plane.

The "first vertex" is a vertex on the polyhedron's equator from which the positions of the others can be calculated.  Its position is calculated:

r = ρ_U sin ψ_h
w = ρ_U cos ψ_h
x = r sin i sin σ
y = r ( sin ω cos σ + cos ω sin σ cos i)
z = r ( cos ω cos σ + sin ω sin σ cos i)

The Planets

Each Heavenly Sphere has one planet, orbiting on the N polygonal equator of the polyhedron.  Given a current angle a of the planet from the first vertex the current distance from the orbit centre is

d = r ( sin c / sin(π-c-a+b) )

where b is the angle from the first vertex to the last passed vertex (V_n), and c is half the interior angle of the polygon.
The planet belonging to the first heavenly sphere orbits in a different pattern.  d is derived

r - ( r sin a / 2 ) or r + ( r sin a / 2 ) [where a > π]

d can be converted into a 3-spherical ψ coordinate or a w coordinate:

ψ = asin(d / ρ_U)
w = ρ_U cos ψ

The remaining coordinates must satisfy w²  + x²  + y²  + z²  = ρ_U² to keep the position on the surface of the 3-sphere.  Rearranged  x²  + y²  + z² = ρ_U² – w² gives a 2-sphere of radius sqrt(ρ_U² – w²).

xyz values can now be derived from the orbital elements:

D = √(ρ_U² – w²)
x = D sin i sin (a+σ)
y = D ( sin ω cos (a+σ) + cos ω sin (a+σ) cos i)
z = D ( cos ω cos (a+σ) + sin ω sin (a+σ) cos i)